Syarat Dua Segitiga Kongruen - Pada bagian sebelumnya, kamu sudah mengetahui bahwa dua segitiga akan kongruen jika sisi-sisi yang bersesuaian sama panjang dan sudut-sudut yang bersesuaian sama besar. Dengan demikian, kamu harus menghitung setiap panjang sisi dan besar sudut kedua segitiga untuk membuktikan kekongruenan dua segitiga tersebut. Tentunya hal ini akan menyita waktu.
Syarat Dua Segitiga Kongruen
A. Sisi-Sisi yang Bersesuaian Sama Panjang (s.s.s)
Amati Gambar A di bawah ini Pada gambar tersebut, AB = PQ, BC = QR, dan AC = PR. Ukurlah besar sudut-sudut dari kedua segitiga tersebut. Dari hasil pengukuran tersebut, kamu akan memperoleh hubungan ¾A = ¾P; ¾B = ¾Q; ¾C = ¾R.
 |
| Gamba A, Segitiga Kongruen |
Dengan demikian, ¾ABC dan ¾PQR memenuhi sifat dua segitiga yang kongruen, yaitu sisi-sisi yang bersesuaian sama panjang dan sudut-sudut yang bersesuaian sama besar.
Jadi, ¾ABC kongruen dengan ¾PQR.
Berdasarkan uraian di atas tampak bahwa jika sisi-sisi yang bersesuaian dari dua segitiga sama panjang maka dua segitiga tersebut kongruen. Apakah hal itu berlaku secara umum?
Ternyata sifat berikut ini sesuai:
Jika sisi-sisi yang bersesuaian dari dua segitiga sama panjang (s.s.s) maka dua segitiga tersebut kongruen.
B. Dua Sisi yang Bersesuaian Sama Panjang dan Sudut yang Diapitnya Sama Besar (s.sd.s)
Amati Gambar B di bawah ini. Pada gambar tersebut, DE = KL, ¾D = ¾K, dan DF = KM. Ukurlah panjang EF dan LM, besar ¾E dan ¾L, serta besar ¾F dan ¾M. Berdasarkan hasil pengukuran tersebut, kamu akan memperoleh hubungan EF = LM, ¾E = ¾L, dan ¾F = ¾M. |
| Gambar B Dua Segitiga Kongruen |
Dengan demikian, pada ¾DEF dan ¾KLM berlaku
(i) DE = KL, EF = LM, DF = KM;
(ii) ¾D = ¾K, ¾E = ¾L, ¾F = ¾M.
Hal ini menunjukkan bahwa ¾DEF dan ¾KLM memenuhi sifat dua segitiga yang kongruen. Jadi, ¾DEF ¾ ¾KLM. Uraian tersebut memperjelas sifat berikut. Jika dua sisi yang bersesuaian dari dua segitiga sama panjang dan sudut yang diapitnya sama besar (s.sd.s) maka kedua segitiga itu kongruen.
Baik, saya lanjutkan artikel mengenai syarat untuk dua segitiga dikatakan kongruen
C. Dua Sudut yang Bersesuaian Sama Besar dan Sisi yang Berada di Antaranya Sama Panjang (sd.s.sd)
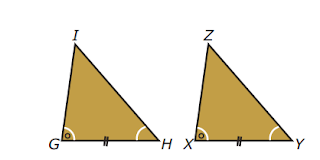 |
| Gambar C Dua Buah Segitiga Kongruen |
Dengan demikian, pada ¾GHI dan ¾XYZ berlaku
(i) ¾G = ¾X, ¾H = ¾Y, dan ¾I = ¾Z;
(ii) GH = XY, HI = YZ, dan GI = XZ.
Hal ini menunjukkan bahwa ¾GHI dan ¾XYZ memenuhi sifat dua segitiga yang kongruen. Jadi, ¾GHI ¾ ¾XYZ.
Berdasarkan uraian tersebut, dapatkah kamu menemukan sifat berikut?
Jika dua sudut yang bersesuaian dari dua segitiga sama besar dan sisi yang berada di antaranya sama panjang (sd.s.sd) maka kedua segitiga itu kongruen.
D. Dua Sudut yang Bersesuaian Sama Besar dan Sisi yang Berada di Hadapannya Sama Panjang (sd.sd.s)
Amati Gambar D di bawah ini Pada gambar tersebut, ¾A = ¾X, ¾B = ¾Y, dan BC = YZ. Ukurlah besar ¾C dan ¾Z, panjang AB dan XY, serta panjang AC dan XZ. Dari hasil pengukuran tersebut, kamu akan memperoleh hubungan ¾C = ¾Z, AB = XY, dan AC = XZ. |
| Gambar D Syarat Dua Segitiga Kongruen |
Dengan demikian, pada ¾ABC dan ¾XYZ berlaku:
(i) ¾A = ¾X, ¾B = ¾Y, dan ¾C = ¾Z;
(ii) AB = XY, BC = YZ, dan AC = XZ.
Hal ini menunjukkan bahwa ¾ABC dan ¾XYZ memenuhi sifat dua segitiga yang kongruen. Jadi, ¾ABC ¾ ¾XYZ.
Berdasarkan uraian tersebut, dapatkah kamu menemukan sifat berikut? Jika dua sudut yang bersesuaian dari dua segitiga sama besar dan satu sisi sekutu kedua sudutnya sama panjang (sd.sd.s) maka kedua segitiga tersebut kongruen.Nah, para pembaca sekalian demikianlah artikel dari Garda Pengetahuan yang berjudul Syarat Dua Segitiga Kongruen, Insya Allah artikel ini bermanfaat.
Syarat Dua Segitiga Kongruen
4/
5
Oleh
Keanekaragaman Indonesia